عدد نپر

برخلاف اکثر اعداد که از طریق هندسی به دست میان عدد نپر از طریق هندسی قابل توضیح نیست. مثلا عدد π از تقسیم محیط هر دایره ای به قطرش به دست میاد ولی داستان عدد نپر چیه؟
عدد e عددی گنگه یعنی مثل عدد π انتها و نظمی نداره. ولی به صورت تقریبی 2.7 درنظر گرفته میشه. عدد 2.7 برای اولین بار در سال 1618 توسط جان نپر مورد استفاده قرار گرفت ولی کشف واقعی این عدد توسط ژاکوب برنولی صورت گرفت. در ابتدا این عدد با نماد c  یا  b نشون داده می شد ولی برای اولین باراویلر در سال 1727 از نماد e  برای نشون دادنش استفاده کرد. در مورد اینکه چرا اویلر از نماد e استفاده کرد، روایات زیادی هست. برخی  e رو اول کلمه exponential به معنای نمایی میدونن. بعضی ها اون رو اول نام اویلر "euler" می دونن. بعضی هم میگن چون حروف a , b ,c, d تا آن زمان خیلی در روابط ریاضی استفاده شده بود، اویلر اون رو با حرف e نشون داده. در هر صورت امروزه نماد عدد 2.7 حرف e می باشد که به اون عدد اویلر یا عدد نپر هم گفته میشه. عدد اویلر برای اولین بار تا 18 رقم اعشار توسط اویلر حساب شد ولی امروز تا 1014 رقم اعشار اون تعیین شده. همونطور که گفتیم عدد نپر از راه هندسی به دست نمیاد و یک نسبت ریاضی هست که در تمامی پدیده هایی که در مورد رشد و تغییر هست دیده میشه. یعنی هر پدیده ای که در حال تغییر هستش وابسته به عدد نپر هستش. مثلا رشد باکتری ها، تغییرات دما، رشد سلول های بدن، رشد پولی که شما در بانک می ذارید تماما وابسته به عدد نپر  هستش.

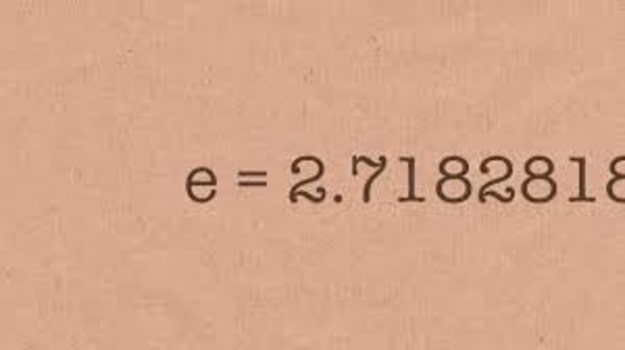
عدد نپر و سود بانکی

در قرن هفدهم، ژاکوب برنولی ریاضی دان و فیزیک دان سوئیسی بسیار علاقه مند به محاسبه سود بانکی بود و دنبال این بود که حداکثر سود بانکی رو محاسبه کنه. در واقع اون دنبال تعیین اثر مرکب رشد بوده که امروزه حتی در امور روانشناسی هم مورد توجه قرار گرفته. سعی می کنیم روش برنولی رو به زبان ساده توضیح بدیم:
فرض کنید شما در بانکی یک دلار پول دارید و اون بانک خیلی دست ودلبازه و سالی 100 درصد سود به شما میده یعنی پول شما رو دو برابر می کنه. در واقع به عبارتی بعد از گذشت  یکسال پول شما میشه 2 دلار. حالا فرض کنید بانک به شما پیشنهاد بده که به جای اینکه سالی 100 درصد سود بده، هر 6 ماه 50 درصد سود رو بده یعنی بعد 6 ماه 50درصد و 6ماه بعد 50 درصد دیگه به شما سود بده. به نظرتون بدتره یا بهتر؟ شما قبول می کردین؟ 
بیاید محاسبه کنیم. بعد 6 ماه 50 درصد سودتون به اضافه پول اولتون میشه 1.5 دلار. 6 ماه بعد 50 درصد به اضافه 1.5 دلارتون میشه 2.25 دلار یعنی بیشتر سود کردین. حالا اگه بانک هر سه ماه، 25 درصد سود بده یعنی سود سالیانه 100 درصد بشه هرسه ماه، 25 درصد  بعد از یک سال چقدر پول داریم؟
اگر محاسبات رو به درستی انجام بدیم میزان پول در بانک تقریبا 2.43 دلاره که میزان سود از حالت شش ماهه هم بیشتره. به همین روش اگه بانک سود رو به صورت روزانه بده بعد یکسال تقریبا 2.714 دلار پول داریم و اگه سود به صورت ساعتی، یا دقیقه ای یا ثانیه ای پرداخت بشه سود به عدد 2.718 میرسه که معادل عدد e هست. درواقع رابطه ای که پول رو بعد از یکسال میشه محاسبه کرد به صورت  (1+1/n) به توان n است. که n تعداد تقسیم هایی هست که قراره انجام بشه. اویلر به جای n، ∞ گذاشت و عدد نپر رو محاسبه کرد. اویلر عدد نپر رو همچنین از رابطه مشهور ...+!e=1+1/1!+1/2 هم به دست آورد و ثابت کرد که این عدد گنگ هستش  یعنی هیچ نظم و انتهایی نداره.

کاربرد عدد نپر

عدد نپر زبان رشد طبیعت هست یعنی هر چیزی که رشد و تغییر داره حتما به عدد نپر وابسته است. در زیست شناسی به کمک عدد نپر و توابع نمایی میزان تکثیر باکتری ها و یا رشد سلول های سرطان قابل محاسبه است. میزان کربن موجود در اشیا وابسته به توابع نمایی و عدد نپر که این امر باعث میشه دانشمندان قادر باشن سن واقعی فسیل ها و اشیا قدیمی رو به راحتی تعیین کنن. میزان قدرت ذرات رادیواکتیو در نیروگاه های هسته ای به کمک عدد  نپر قابل محاسبه است. روزانه اتفاقات زیادی دور و برمون میفته که وابسته به عدد نپر هستش مثلا برای همه ما اتفاق افتاده که منتظر خنک شدن جسم داغی مثل چایی یا قهوه و یا غذایی که از فر خارج شده باشیم. جالبه که سرعت خنک شدن اجسام در محیط با عدد e نسبت داره. عدد نپردر پدیده های تصادفی هم زیاد دیده میشه. مثلا فرض کنید احتمال برنده شدن در یک قرعه کشی، 1/1000000 باشد. اگر 1000000 بار قرعه کشی بشه احتمال اینکه شما در این قرعه کشی اسمتون درنیاد تقریبا برابر 1 برروی e هستش یا تقریبا 37 درصده. فرض کنید در یک مهمونی همه با چتر وارد میشن و چتر ها رو در اتاقی قرار میدن. و در آخر مهمونی هرکس به صورت تصادفی یک چتر رو برمیداره . اگه تعداد مهونا نسبتا زیاد باشه، احتمال اینکه هیچکس چتر خودش رو برنداشته باشه بازهم همون نسبت هست.
مثال دیگه فرض کنید یک دست ورق رو به صورت مرتب می چینیم و بعد شروع به قاطی کردن اونا می کنیم. احتمال اینکه هیچکدوم از ورق ها سرجاشون قرار نگیره باز هم همون 1 بر روی e هست.

زیباترین معادله ریاضی

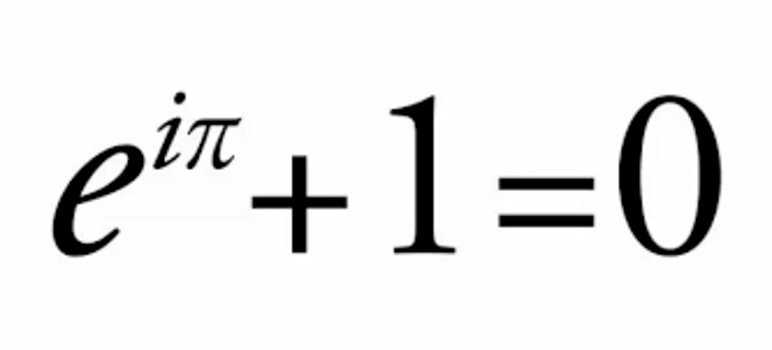
زیبا ترین معادله ریاضی رو معادله بالا  می دونن چون مهم ترین اعداد ریاضی یعنی عدد نپر e، عدد مختلط i، عدد پی، عدد 1 و عدد صفر در اون استفاده شده.

سخن پایانی:

شاید عدد نپر به اندازه عدد پی معروف نباشه ولی همونطور که دیدین نقش اساسی در پدیده های دور و برمون داره. 

سوالات متداول

• کاربرد عدد  نپر در ریاضیات

• تتعریف عدد نپر در ریاضی

• ویژگی های عدد نپر

برای رزرو و ثبت نام جلسات مشاوره تحصیلی بارسا
( مشاوره تحصیلی تلفنی و حضوری ) با شماره ۲۲۶۷۷۹۱۷-۰۲۱ تماس بگیرید
یا عدد ۶۶ را به سامانه ۳۰۰۰۹۰۹۰۳۰ ارسال کنید.